转载-进制转换
进制转换
二进制 → 十进制
将二进制的 101011 转换为十进制的步骤如下:
- 第 0 位:1 * 2 ^ 0 = 1;
- 第 1 位:1 * 2 ^ 1 = 2;
- 第 2 位:0 * 2 ^ 2 = 0;
- 第 3 位: 1 * 2 ^ 3 = 8;
- 第 4 位:0 * 2 ^ 4 = 0;
- 第 5 位:1 * 2 ^ 5 = 32;
- 读数:把结果值相加,1 + 2 + 0 + 8 + 0 + 32 = 43,即(101011)B=(43)D。
八进制 → 十进制
八进制就是逢8进1,八进制数采用 0~7 这八数来表达一个数
将八进制的(53)O转换为十进制的步骤如下:
- 第 0 位:3 * 8 ^ 0 = 3;
- 第 1 位:5 * 8 ^ 1 = 40;
- 读数:结果值相加,3 + 40 = 43;即(53)O=(43)D。
十六进制 → 十进制
十六进制就是逢16进1,十六进制的16个数为0123456789ABCDEF。
将十六进制的(2B)H转换为十进制的步骤如下:
- 第 0 位 B x 16^0 = 11;(从 9 往后,A是10,B是11)
- 第 1 位 2 x 16^1 = 32;
- 读数:把结果值相加,11 + 32 = 43,即(2B)H=(43)D。
十进制 → 二进制
除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
将十进制的 43 转换为二进制的步骤如下:
- 将商 43 除以 2 ,商 21 余数为 1;
- 将商 21 除以 2,商 10 余数为 1;
- 将商 10 除以 2 ,商 5 余数为 0;
- 将商 5 除以 2,商 2 余数为 1;
- 将商 2 除以 2,商 1 余数为 0;
- 将商 1 除以 2,商 0 余数为1;
- 读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,101011,即(43)D=(101011)B。

十进制 → 八进制
除8取余法,即每次将整数部分除以8,余数为该位权上的数,而商继续除以8,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数起,一直到最前面的一个余数。
将十进制的(796)D转换为八进制的步骤如下:
- 将 796 除以 8,商 99 余数为 4;
- 将 99 除以 8,商 12 余数为 3;
- 将 12 除以 8,商 1 余数为 4;
- 将 1 除以 8 ,商 0 余数为 1;
- 读数,因为最后一位是经过多次除以8才得到的,因此它是最高位,读数字从最后的余数向前读,1434,即(796)D=(1434)O。
十进制 → 十六进制
除16取余法,即每次将整数部分除以16,余数为该位权上的数,而商继续除以16,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数起,一直到最前面的一个余数。
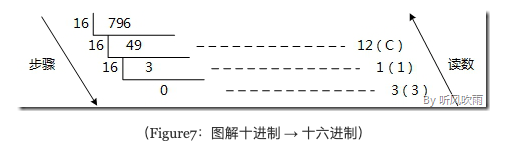
将十进制的(796)D转换为十六进制的步骤如下:
- 将 796 除以 16,商 49 余数为 12,对应十六进制的C
- 将 49 除以 16,商 3 余数为 1
- 将3 除以 16,商 0 余数为 3
- 读数:因为最后一位是经过多次除以16才得到的,因此它是最高位,读数字从最后的余数向前读,31C,即(796)D=(31C)H。