常见排序算法

发表于 分类于 / Changyan：

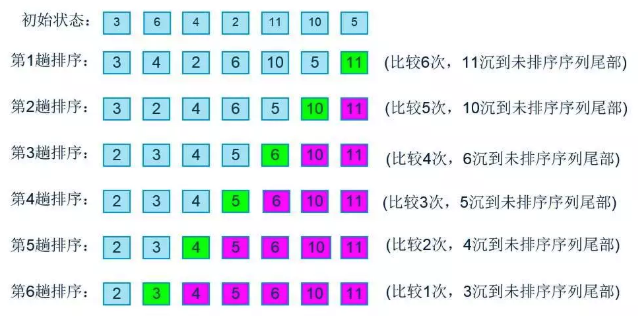
冒泡排序

冒泡排序是一种交换排序，基本思想是：两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。

算法步骤

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

动图演示

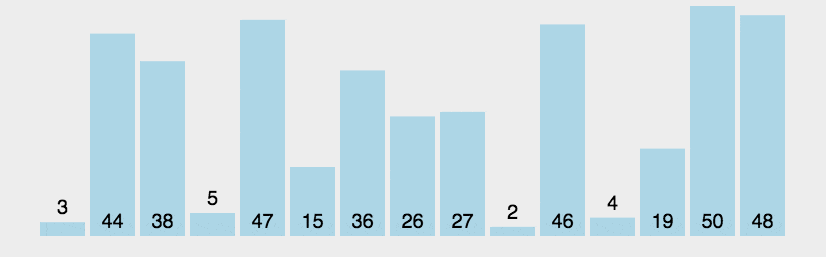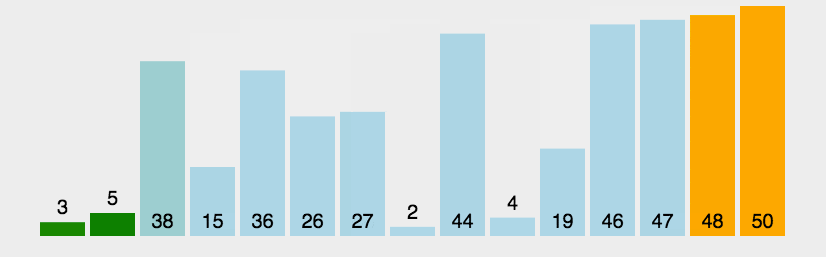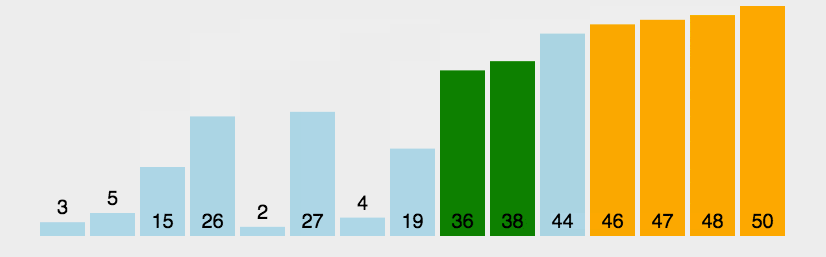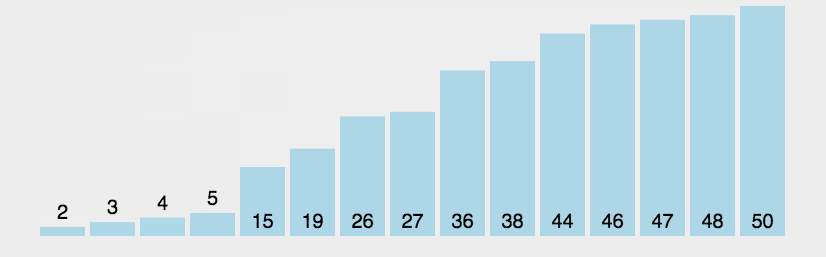
———— 动图来自《菜鸟教程》

说明：绿色表示当前正在比较的两个相邻元素；橘黄色表示已排完序的元素，不再参与后续的比较

代码实现（JS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

function myBubbleSort(arr) {
    var len = arr.length, temp;
    for (var i = 0; i < len - 1; i++) { // 趟数
        for (var j = 0; j < len - 1 - i; j++) { // 当前趟要比较的次数
            if (arr[j] > arr[j+1]) {        // 相邻元素两两比较
                temp = arr[j];              // 元素交换
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
    return arr;
}

代码与图片配合食用更加~

选择排序

选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

算法步骤

  1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
  2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  3. 重复第2步，直到所有元素均排序完毕。

动图演示

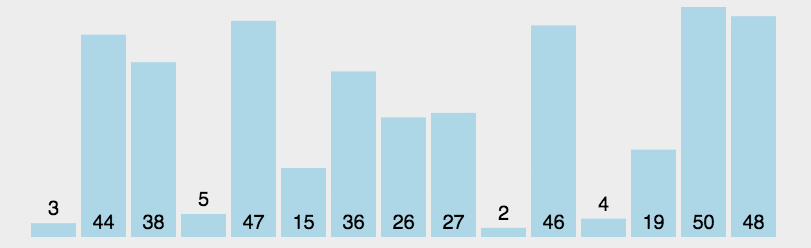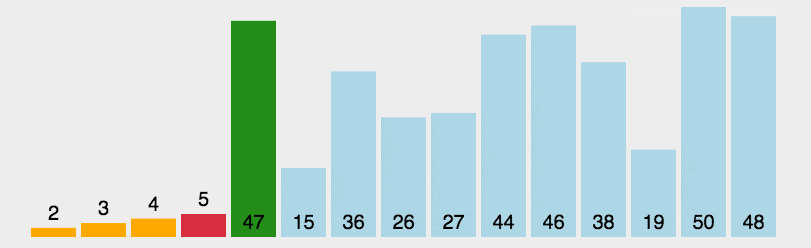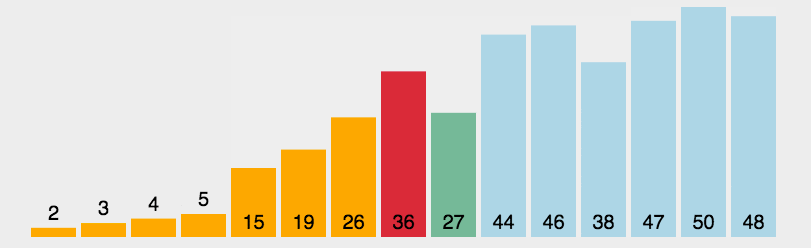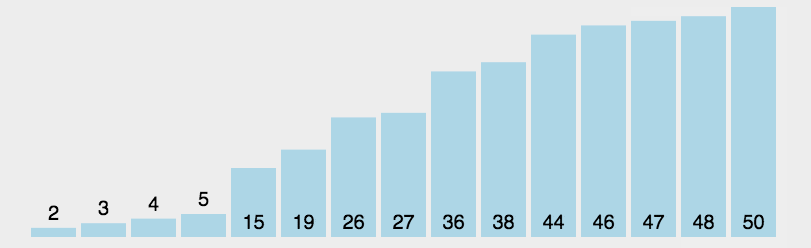
代码实现（JS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

function mySelectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {       // 第 i 轮选择
        minIndex = i;                         // 每轮开始假设起始元素为最小值
        for (var j = i + 1; j < len; j++) {   // 遍历剩余未排序元素
            if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                minIndex = j;                 // 将最小数的索引保存
            }
        }
        temp = arr[i];                         // 交换起始元素与真正的最小值
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

配图：

插入排序

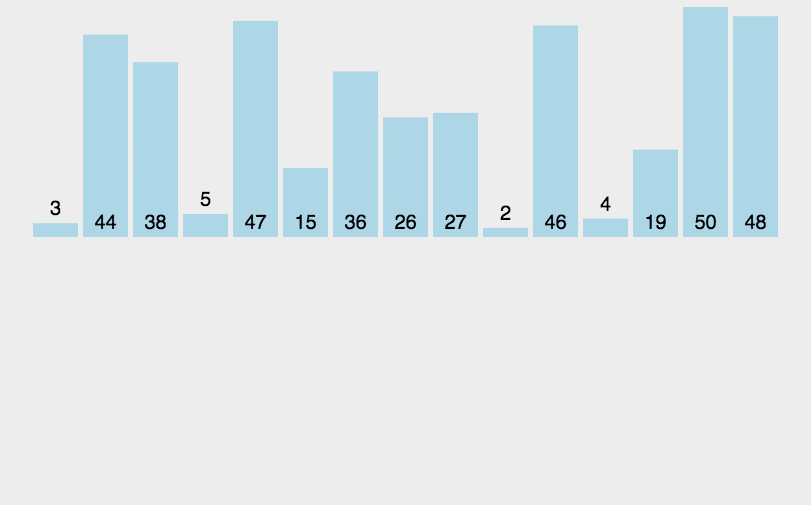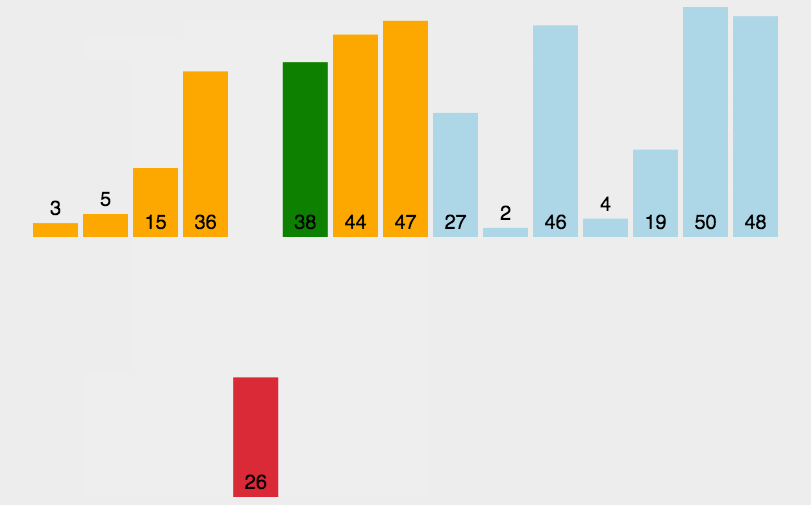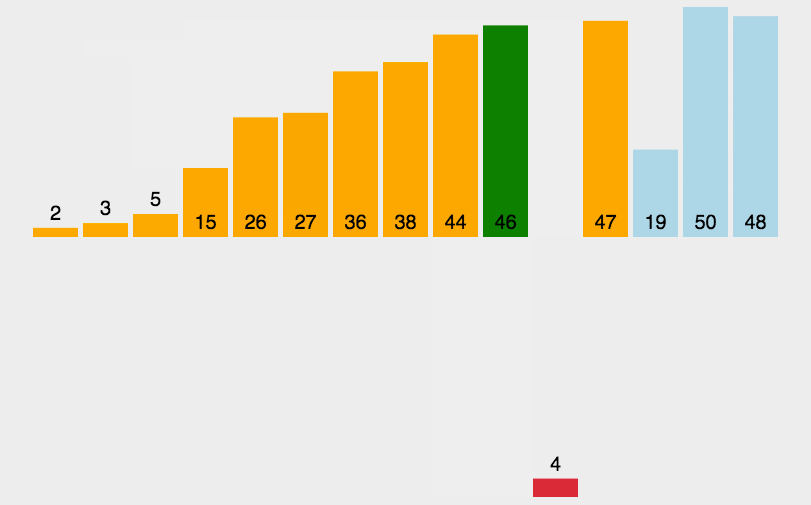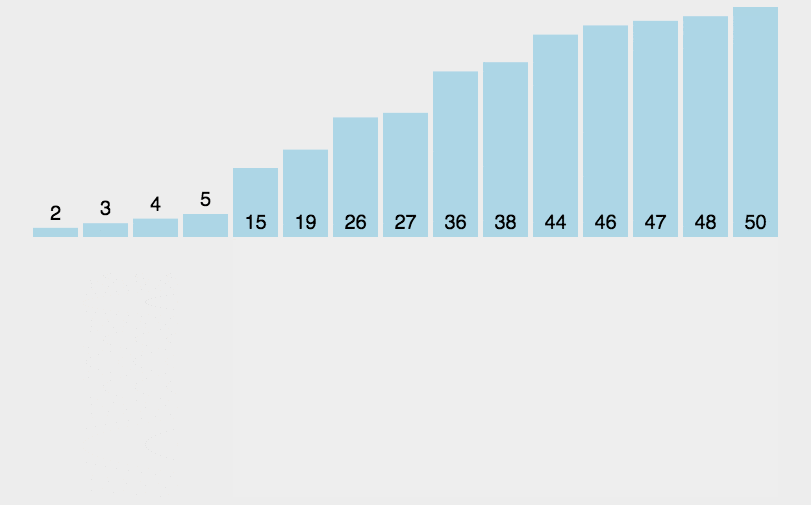
插入排序的原理应该是最容易理解的，因为只要你打过扑克牌就应该能秒懂。插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

算法步骤

  1. 从第一个元素开始，该元素可以认为已经被排序；
  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置；
  4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
  5. 将新元素插入到该位置后；
  6. 重复步骤2~5。

动图演示

代码实现（JS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

function myInsertSort(arr) {
    var len = arr.length;
    var insertItem; // 要插入的元素

    // 从数组的第二个元素开始循环将数组中的元素插入
    for (var i = 1; i < len; i++) {
        insertItem = arr[i]; // 设置数组中的第2个元素为第一次遍历要插入的数据
        var j = i - 1;       // 已排序好数组的最后一个元素的索引

        // 将已排好序的元素从最后一个往前依次与待插入元素比较，
        while (j >= 0 && insertItem < arr[j]) {
            // 如果要插入的元素小于第j个元素,就将第j个元素向后移动
            arr[j + 1] = arr[j];
            j--;
        }
        // 直到要插入的元素不小于第j个元素,将insertNote插入到数组中
        arr[j + 1] = insertItem;
    }
    return arr;
}
// 例如for循环中 i 等于 2 时，已排序完毕的元素为[3,44]，进入for循环
    // 待插入元素为 arr[2]，也就是38;
    // j=i-1也就是2-1等于1
    // while循环比较，待插入元素38是小于arr[j]（j=1）44 的 => 条件成立
        // arr[j+1]要等于arr[j] => arr[2]要等于arr[1] => arr[2]=44 => 此刻数组前三个元素：[3,44,44]
        // j-- => j=1-1也就是0
    // 再来一轮while比较，待插入元素38现在不小于arr[j] 也就是arr[0]的3，所以直接退出while循环
    // arr[j+1]=insertItem => arr[1]=38 => 数组前三排序完毕：[3,38,44]

希尔排序

希尔排序也是一种插入排序，它是简单插入排序的一个改进版，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。本文会以图解的方式详细介绍希尔排序的基本思想及其代码实现。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

算法步骤(示例)

在此我们选择增量 gap=数组长度length/2，缩小增量继续以 gap = gap/2 的方式，这种增量选择我们可以用一个序列来表示：{n/2,(n/2)/2...1}，称为增量序列。当然，希尔排序的增量序列有很多种，这里采用的是比较常用的一种作为示例：

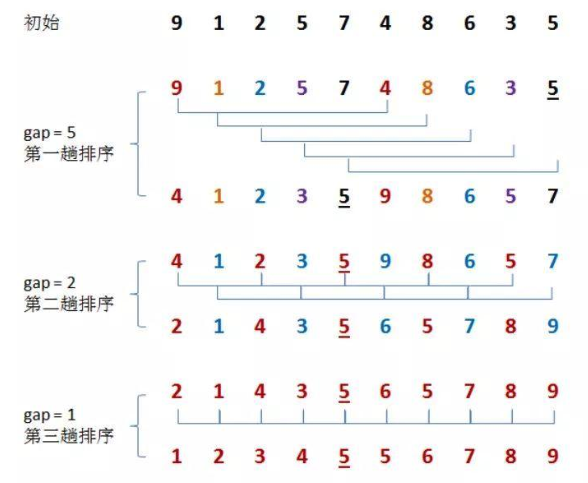
在上面这幅图中：

初始时，有一个大小为 10 的无序序列。

在第一趟排序中，我们设 gap1 = 10 / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。接下来，按照直接插入排序的方法对每个组进行排序。

在第二趟排序中，我们把上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整)。这样每相隔距离为 2 的元素组成一组，可以分为 2 组。按照直接插入排序的方法对每个组进行排序。

在第三趟排序中，再次把 gap 缩小一半，即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组，即只有一组。按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

注意：图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到，在排序过程中，两个元素位置交换了。
所以，希尔排序是不稳定的算法。

代码演示（JS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

function myShellSort(arr) {
    var gap = Math.floor(arr.length / 2);

    while (1 <= gap) {
        // 把距离为 gap 的元素编为一个组，扫描所有组
        for (var i = gap; i < arr.length; i++) {
            var j = 0;
            var temp = arr[i];

            // 对距离为 gap 的元素组进行排序
            for (j = i - gap; j >= 0 && temp < arr[j]; j = j - gap) {
                arr[j + gap] = arr[j];
            }
            arr[j + gap] = temp;
        }

        console.log(`gap = ${gap}`);
        console.log(arr);
        gap = Math.floor(gap / 2); // 减小增量
    }
    return arr;
}

归并排序

归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治策略（分治法将问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段得到的各答案”修补”在一起，即分而治之)。

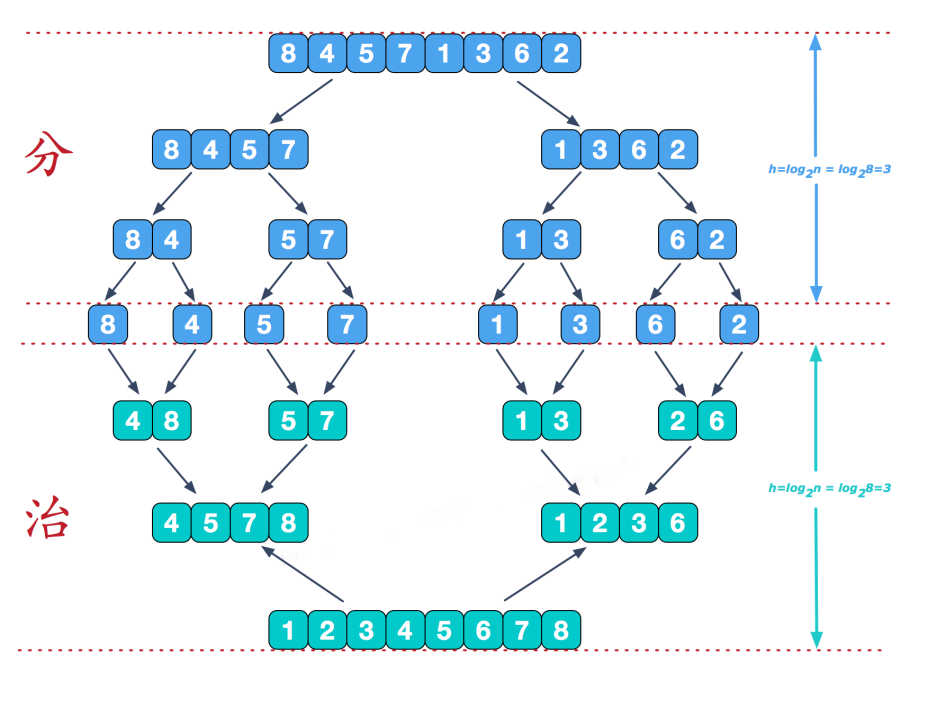
可以看到这种结构很像一棵完全二叉树，下面的归并排序代码将会采用递归去实现（你也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为logn。

算法步骤

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
  4. 重复步骤 3 直到某一指针达到序列尾
  5. 将另一序列剩下的所有元素直接复制到合并序列尾

图片演示

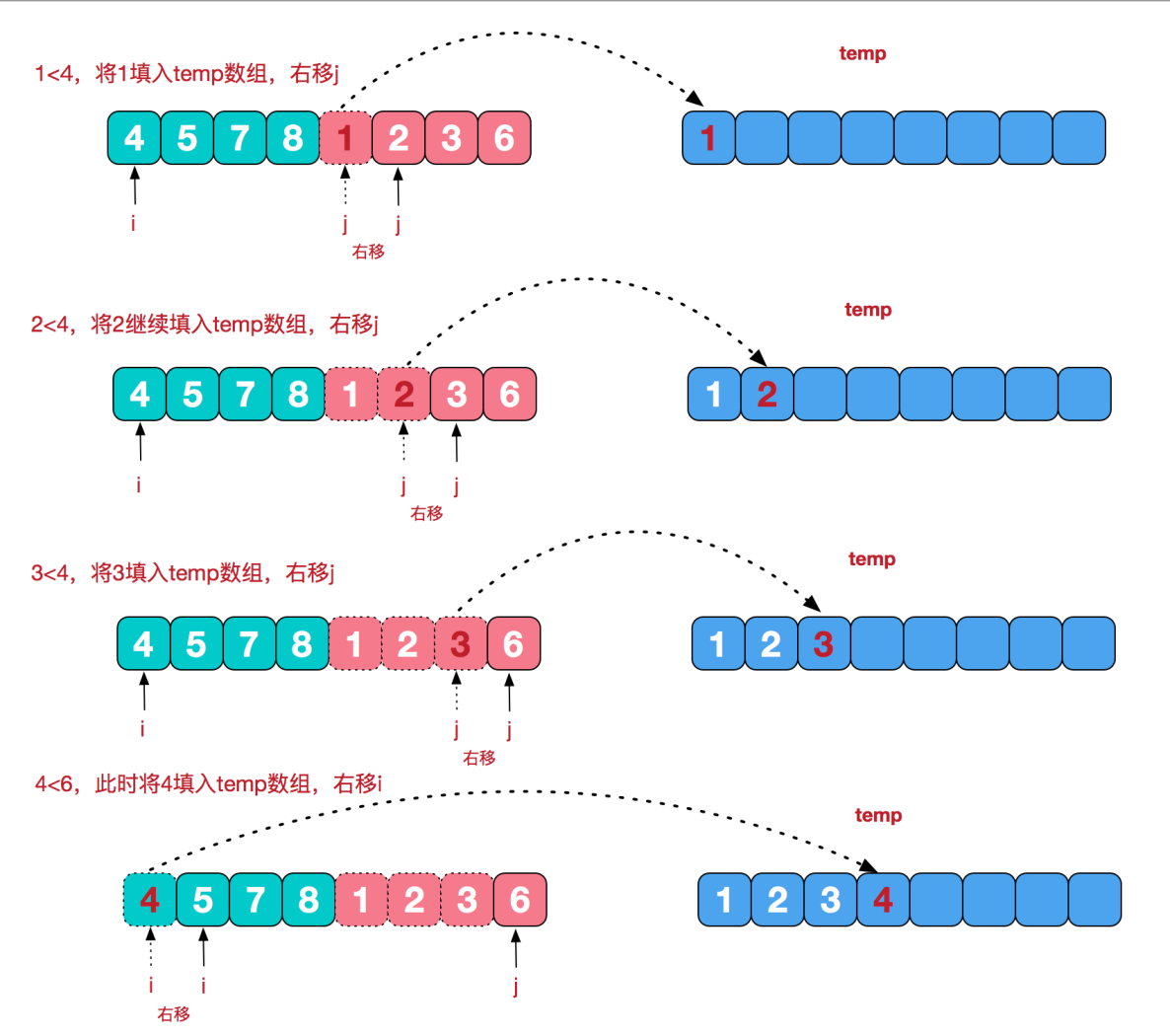
图片来自博客《图解排序算法之归并排序》

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

function mergeSort(arr) { // 采用自上而下的递归方法
    var len = arr.length;
    if (len < 2) return arr;
  
    var middle = Math.floor(len / 2), // 将未排序数组拆分成两半分而治之
        left = arr.slice(0, middle),
        right = arr.slice(middle);
  
    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
    var result = [];

    while (left.length && right.length) {
      	// 两边的起始元素相互比较，始终将小的一方的头元素弹出，并push到准备好的容器result中
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
        }
    }

    while (left.length)
        result.push(left.shift());

    while (right.length)
        result.push(right.shift());

    return result;
}

快速排序

快速排序的基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的元素均比另一部分记录的元素小，继而再分别对这两部分记录递归的进行同样的排序操作。

算法步骤

  1. 把数组中第一个元素当做一个基准值，称为“基准”（Pivot）
  1. 重新排序数列，把所有比基准值小的元素摆放在基准前面，所有比基准值大元素摆放在基准后面。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  1. 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序；

分区（Partition）思路

首先把未排序数组的第一个（最左边）元素设置为基准，把它的位置叫做 l ：

然后依次向后查看所有元素，在查看过程中，不断的调整后面元素的位置，使得后面的元素分为两部分，一部分都小于 v ；一部分都大于 v 。

我们用 j 来不断记录这两部分的分割线位置。而 e 就是我们要判断的下一个元素，用索引 i 来表示，i 会遍历每一个元素，来看该如何调整这个元素。

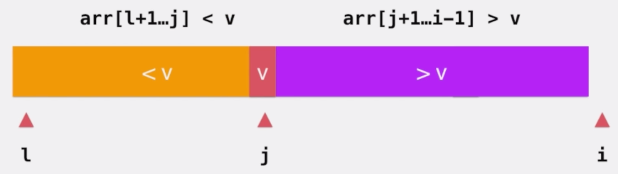
在下图中，我们用 arr[l+1 ... j] 来表示小于 v 的橙色部分，用 arr[j+1 ... i-1] 来表示大于 v 的紫色部分。

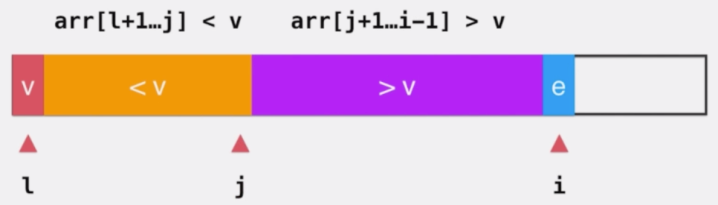
接下来就要看如何来调整下一个元素 e 的位置。分情况讨论：

当 e 大于 v 时，我们直接让 e 融入大于 v 的部分，并让 i++

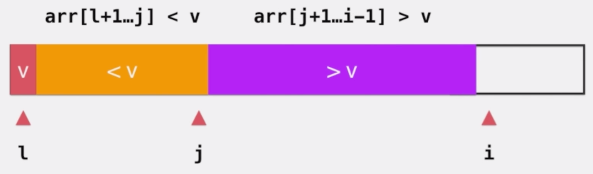
当 e 小于 v 时，我们让 e 和大于 v 部分的第一个元素交换位置。

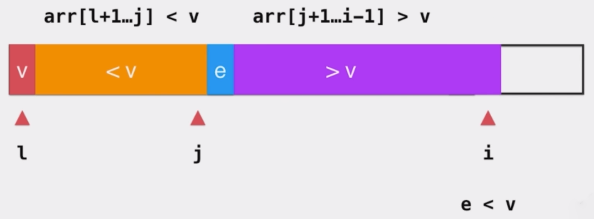
把 e 融入到小于 v 的部分。此时就需要让分隔线的索引位置 j++ ，相应的，索引 i 的位置也要 i++ 以便查看下一个元素。

以这样的步骤我们就能遍历完整个数组，如下图所示

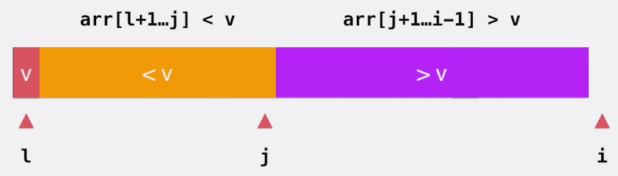
现在还差最后一个步骤，那就是把基准值 v ，与小于 v 部分的最后一个元素交换位置。此刻 v 左边都小于它，v 右边都大于它，而 j 指向的就是基准值所在的位置。这样我们就完成了分区（Partition）操作。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

function quickSort(arr, left, right) {
    var len = arr.length,
        partitionIndex,         // 分区索引
        left = typeof left != 'number' ? 0 : left,
        right = typeof right != 'number' ? len - 1 : right;

    if (left >= right) return;

    // 通过分区找到分隔点，再分别快排左右两部分
    partitionIndex = partition(arr, left, right);
    quickSort(arr, left, partitionIndex - 1);
    quickSort(arr, partitionIndex + 1, right);
    return arr;
}

function partition(arr, left, right) { // 分区操作
    var v = left,   // 设定基准值（pivot）
        j = left;  // arr[l+1...j] ; arr[j+1...i]
    for (var i = j + 1; i <= right; i++) {
        if (arr[i] < arr[v]) { // 当前要判断元素 小于 基准元素时
            j++; // 分隔点右移
            swap(arr, i, j);   // 让 当前元素 与大于 v 部分的第一个元素交换位置
        }
        // 此处不用写 else ，因为当大于基准元素时，直接i++就好，
        // 而i++，for循环已经帮我们做了
    }
    // 循环完毕后，交换基准值和小于v部分的最后一个元素的位置
    swap(arr, v, j);
    return j;
}

function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

console.log(quickSort(arr, 0, arr.length));

计数排序

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

算法步骤

  1. 找出待排序的数组中最大和最小的元素；
  2. 统计数组中每个值为 i 的元素出现的次数，存入数组 Count 的第 i 项；
  3. 对所有的计数累加（从 Count 中的第一个元素开始，每一项和前一项相加）；
  4. 反向填充目标数组：将每个元素 i 放在新数组的第 Count(i) 项，每放一个元素就将 Count(i) 减去1。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

function countingSort(arr) {
    var len = arr.length,
        Result = [],
        Count = [],
        min = max = arr[0];

    // 查找最大最小值,并将arr数置入Count数组中,统计出现次数
    for (var i = 0; i < len; i++) {
        min = min <= arr[i] ? min : arr[i];
        max = max >= arr[i] ? max : arr[i];
        Count[arr[i]] = Count[arr[i]] ? Count[arr[i]] + 1 : 1;
    }

    // 从最小值->最大值,将计数逐项相加
    for (var j = min; j < max; j++) {
        Count[j + 1] = (Count[j + 1] || 0) + (Count[j] || 0);
    }
    // Count中,下标为arr数值,数据为arr数值出现次数;反向填充数据进入Result数据
    for (var k = len - 1; k >= 0; k--) {
        // Result[位置] = arr数据
        Result[Count[arr[k]] - 1] = arr[k];
        // 减少Count数组中保存的计数
        Count[arr[k]]--;
    }
    return Result;
}

console.log(countingSort(arr));