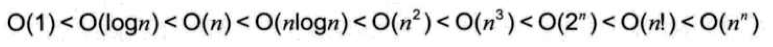<大话数据结构>笔记
前言
之前对算法和数据结构没有一个系统的学习,从今天开始抽空啃啃书吧。就从这本程杰老师的《大话数据结构》起步。
p.s. 原笔记是存放在幕布上的,文字版看着不舒服可以 点击这里 看思维导图版。
数据结构绪论
- 基本概念和术语
- 数据
- 定义:是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的集合符号。
- 总结:数据即符号,必备条件:
- 可以输入到计算机中
- 能被计算机程序处理
- 举例:
- MP3是声音数据
- 图片是图像数据
- #数据对象
- 定义:是性质相同的数据元素的集合,是数据的子集
- 举例:
- 人(都有姓名、生日等相同的数据项)
- #数据元素
- 定义:是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理。也被成为记录。
- 举例:
- 人类中的人
- 畜类中的牛马羊
- #数据项
- 定义:一个数据元素可以由若干个数据项组成
- 举例:
- 人的姓名、年龄、性别
- 数据结构
- 定义:是相互之间存在一种或多种特定关系的数据元素的集合
- #逻辑结构
- 定义:指数据对象中数据元素之间的相互关系
- 类型
- #集合结构
- 同属于一个集合的数据元素
- 同属于一个集合的数据元素
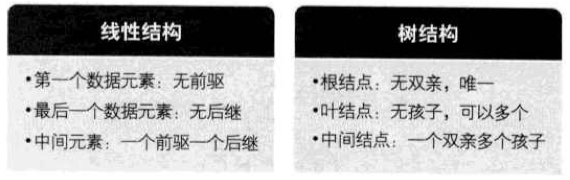
- #线性结构
- 数据元素之间是一对一的关系
- 数据元素之间是一对一的关系
- #树形结构
- 数据元素之间存在一对多的层次关系
- 数据元素之间存在一对多的层次关系
- #图形结构
- 数据元素是多对多的关系
- 数据元素是多对多的关系
- #集合结构
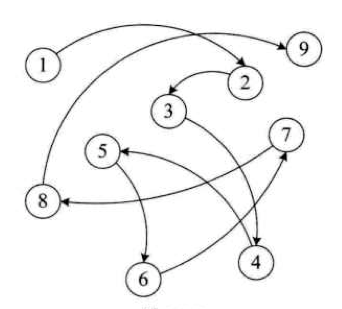
- 用示意图表示数据逻辑结构时的注意点:
- 每个数据元素是一个结点,用圆圈表示
- 元素之间的逻辑关系用连线表示,如果此关系是有方向的,那么用箭头连线表示
- #物理结构
- 定义:是指数据的逻辑结构在计算机中的存储形式
- #顺序存储结构
- 定义:是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的
- 定义:是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的
- #链式存储结构
- 定义:是把数据元素存放在任意的存储单元里,这组存储单元可以使连续的,也可以是不连续的。
- 注意:数据元素的存储关系并不能反映其逻辑关系,因此需要用一个指针存放数据元素的地址,这样通过地址就可以找到相关联数据元素的位置
- 定义:是把数据元素存放在任意的存储单元里,这组存储单元可以使连续的,也可以是不连续的。
- 数据
- 基本概念和术语
算法
- 基本特性:输入、输出、有穷性、确定性和可行性
- 设计要求:正确性、可读性、健壮性、高效和低存储量
- 度量方法:事后统计(不科学、不准确)、事前分析估算 ✅
- 时间复杂度
- 概念
- 计算公式:T(n) = O(f(n))
- T(n): 语句总的执行次数
- n: 问题规模
- f(n): 问题规模 n 的某个函数
- 表示随问题规模 n 的增大,算法执行时间的增长率和 f(n) 的增长率相同
- 计算公式:T(n) = O(f(n))
- 大O记法
- 定义:用大写O()来体现时间复杂度,简称为大O记法
- 推导大O阶方法:
- \1. 用常数 1 取代运行时间中的所有加法常数
- \2. 在修改后的运行次数函数中,只保留最高阶项
- \3. 如果最高阶项存在且不是 1,则去除与这个项相乘的常数
- \4. 得到的结果就是大 O 阶
- 常数阶
- 举例:高斯算法

- 此算法运行次数函数是 f(n)=3
- 推导:把常数项 3 改为 1 => 它没有最高阶 => 复杂度:O(1)
- 举例:高斯算法
- 线性阶
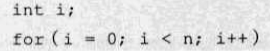
- 推导:循环体中代码需要执行 n 次 => 复杂度:O(n)
- 对数阶

- 推导:每次 count 乘以 2 后,就距离 n 更近一分。换句话说,有多少个 2 相乘后大于 n,则会退出循环。由 2^x=n 得到 x=log(2)n。所以此循环复杂度:O(logn)
- 平方阶
- 举例1

- 推导:两层循环,每层循环 n 次 => 复杂度:O(n^2)
- 如果把外层 n 改为 m,则复杂度:O(m✘n)
- 举例2

- 复杂度:O(n^2)
- 举例1
- 常见时间复杂度
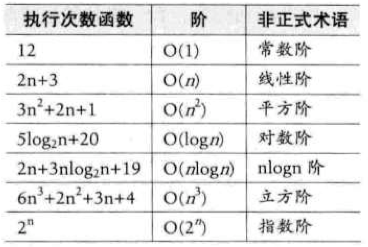
- 常见时间复杂度所耗费的时间从小到大:
- 概念
- 空间复杂度
- 概念
- 计算公式:S(n) = O(f(n))
- S(n):计算算法所耗的存储空间
- n: 问题规模
- f(n): 问题规模 n 所占存储空间的函数
- 计算公式:S(n) = O(f(n))
- 概念
- 当不用限定词地使用“复杂度”时,指的都是时间复杂度
- 心得
- 明白算法的时间复杂度估算很重要,不要以“CPU越来越快,不用考虑算法优劣”为借口。愚公移山固然可敬,但发明炸药和推土机更加实在和聪明
线性表
- 定义:零个或多个数据元素的有限序列
- 关键点:
- 是一个有顺序的序列
- 若元素存在多个,则第一个无前驱,最后一个无后继,中间部分都有且只有一个前驱和后继
- 线性表是有限的
- 关键点:
- 举例:
- 幼儿园小朋友按次序排队,各自都知道他前面人是谁,方便清点人数,知道谁不在
- 一年的星座列表
- 顺序存储结构
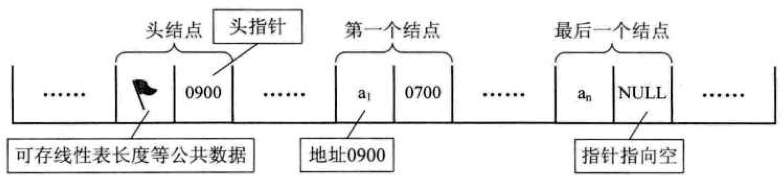
- 定义:用一段地址连续的存储单元一次存储线性表的数据元素
- 三个重要属性:
- 存储空间的起始位置
- 线性表的最大存储容量
- 线性表的当前长度
- 数据长度与线性表长度区别
- 数据长度:(例如一个数组的长度)是存放线性表的存储空间的长度,一般不变
- 线性表长度:是线性表中数据元素的个数,随着插入与删除,这个量是可变的
- 在任意时刻,线性表长度应该 小于等于 数据长度
- 时间复杂度:
- 插入或删除最后一个元素为 O(1)
- 插入或删除第一个元素为O(n)
- 优缺点
- 优点:
- 无需为了表示表中元素之间的逻辑关系而增加额外的存储空间
- 可以快速地存取表中任意位置的元素
- 缺点:
- 插入和删除操作需要移动大量元素
- 当线性表长度变化较大时,难以确定存储空间的容量
- 造成存储空间的“碎片”
- 优点:
- 定义:用一段地址连续的存储单元一次存储线性表的数据元素
- 链式存储结构
- 定义:是把数据元素存放在任意的存储单元里,这组存储单元可以使连续的,也可以是不连续的。
- 与顺序结构不同,在链式结构中,除了要存储数据信息外,还要存储它后继元素的存储地址
- 单链表
- 定义:一个链式结构的,每个结点中只包含一个指针域的链表叫做单链表
- 单链表结构与顺序存储结构的优缺点
- 对比:
- 存储分配方式:
- 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素
- 单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素
- 时间性能:
- 查找:
- 顺序存储结构 O(1)
- 单链表 O(n)
- 插入与删除:
- 顺序存储结构需要移动表长一半的元素,时间为 O(n)
- 单链表在找出某位置的指针后,插入和删除时间仅为 O(1)
- 空间性能:
- 顺序存储结构需要预分配存储空间,分大了浪费,分小了容易溢出
- 单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制
- 查找:
- 存储分配方式:
- 结论:
- 若线性表需要频繁查找,很少进行插入和删除操作,宜采用顺序存储结构
- 若需要频繁插入和删除,宜采用单链表结构
- 当线性表中的元素个数变化较大或根本不知道多大时,宜采用单链表结构,这样不用考虑存储空间的大小问题。
- 若事先知道大致长度,比如一年12个月,一周7天,宜采用顺序存储结构
- 实际应用:
- 用户注册的个人信息,除了注册时插入数据外,绝大多数情况都是读取,所以宜采用顺序存储结构
- 游戏中玩家的武器装备列表,随着游戏推进,玩家可能随时增加或删除,所以宜采用单链表结构
- 对比:
- 定义:一个链式结构的,每个结点中只包含一个指针域的链表叫做单链表
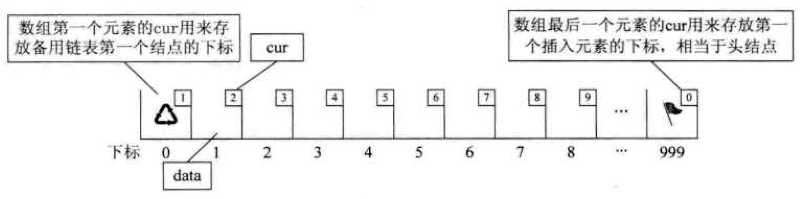
- 静态链表
- 背景:有些编程高级语言(e.g. Basic, Fortran)没有指针,这样链表结构就没法实现。
- 解决方案:用数组来代替指针,来描述单链表
- 实现:让数组元素都由两个数据域组成,data和cur。data用来存储数据元素,cur(游标)相当于单链表中的next指针,存放该元素的后继在数组中的下标。
- 定义:这种用数组描述的链表叫做静态链表。这种描述方法起名为游标实现法。
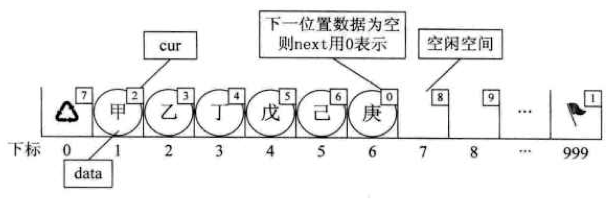
- 举例:
- 将 “甲乙丙丁戊己庚”存入静态链表:
- 优缺点:
- 优点:
- 再插入和删除操作时,只需要修改游标,不需要移动元素,从而改进了在顺序存储结构中的插入和删除操作需要移动大量元素的缺点。
- 缺点:
- 没有解决连续存储分配带来的表长难以确定的问题
- 失去了顺序存储结构随机存储的特性
- 优点:
- 将 “甲乙丙丁戊己庚”存入静态链表:
- 循环链表
- 定义:将单链表中终端节点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表。
- 双向链表
- 定义:双向链表是在单链表的每个结点中,再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域,一个指向直接后继,另一个指向直接前驱。
- 定义:是把数据元素存放在任意的存储单元里,这组存储单元可以使连续的,也可以是不连续的。
- 定义:零个或多个数据元素的有限序列
栈与队列
栈
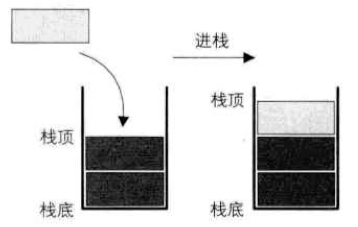
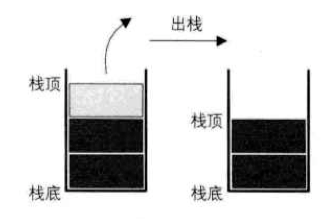
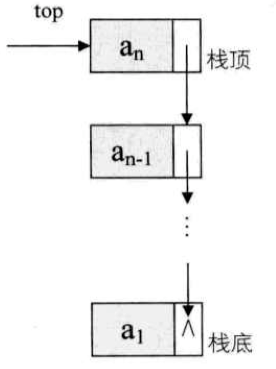
- 定义:栈是限定仅在表尾进行插入和删除操作的线性表
- 描述:我们把允许插入和删除的一端称为栈顶,另一端称为栈底,不含任何数据元素的栈称为空栈。栈又称为后进先出(Last In First Out)的线性表,简称 LIFO 结构。
- 举例:浏览器的前进后退,Photoshop 的前进撤销。
- 栈的顺序存储结构
- 操作:
- 栈的插入操作(push 压),叫作进栈,也称压栈、入栈。类似子弹入弹夹。
- 栈的删除操作(pop 弹),叫作出栈,也称弹栈。类似子弹出夹。
- 栈的插入操作(push 压),叫作进栈,也称压栈、入栈。类似子弹入弹夹。
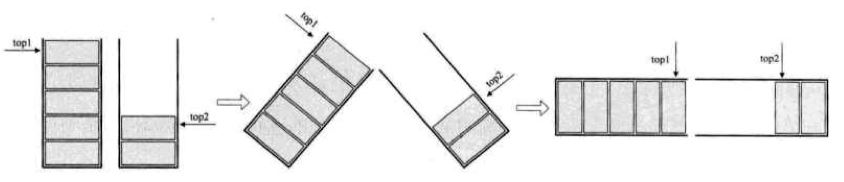
- 两栈共享空间
- 理解:两个相同类型的栈,为它们各自开辟了数组空间,极有可能第一个栈满,再进栈就溢出了,而另一个栈还有很多存储空间空闲。所以我们完全可以用一个数组来存储两个栈。
- 做法:数组的两个端点,让一个栈的栈底为数组的始端(下标0),另一个栈为栈的末端(n-1)。两栈如果增加元素,就是两端向中间延伸。
- 关键思路:
- \1. 两个top是数组两端的栈顶指针,只要它俩不见面,两个栈就都可以一直使用。
- \2. 栈1为空时,就是top1等于-1时;当top2等于n时,即是栈2为空时。
- \3. 何时栈满:top1等于n-1时栈1满;top2等于0时,栈2满,所以推导出,top1+1==top2为栈满
- 理解:两个相同类型的栈,为它们各自开辟了数组空间,极有可能第一个栈满,再进栈就溢出了,而另一个栈还有很多存储空间空闲。所以我们完全可以用一个数组来存储两个栈。
- 操作:
- 栈的链式存储结构
- 栈顶存放位置:
- 由于单链表有头指针,而栈顶指针也是必须的,所以把它俩合二为一,将栈顶放在单链表的头部。
- 不需要头结点:
- 都已经有了栈顶在头部,所以单链表的头结点也失去了意义,所以不需要头结点。
- 示意图:
- 栈顶存放位置:
- 栈的应用
- #递归
- #四则运算表达式求值
队列
定义:队列是只允许在一端进行插入操作、而在另一端进行删除操作的线性表
描述:队列是一种先进先出(First In First Out)的线性表,简称 FIFO。允许插入的一端称为队尾,允许删除的一端称为队头。
举例:键盘的输入,记事本上的输出。
队列的顺序存储结构
缺点:
由于从队头出,导致后面元素都得向前移动,时间复杂度 O(n)

解决:
- 循环队列
- 让头尾相接
- 循环队列
队列的链式存储结构
顺序存储和链式存储的选择
- 可以确定队列长度最大值时,建议循环队列
- 无法预估队列长度时,使用链队列
串
- 定义:是由零个或多个字符组成的有限序列,又名字符串
- 算法
- 朴素的模式匹配算法
- 从头开始依次往后比较【不推荐】
- KMP模式匹配算法
- 朴素的模式匹配算法
数
定义:
- 树是 n(n>=0) 个结点的有限集。n=0 时称为空树。在任意一棵非空树中:
- \1. 有且仅有一个特定的称为根(Root)的结点
- \2. 当 n > 1 时,其余结点可分为 m(m > 0) 个互不相交的有限集 T1、T2 … 、Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)
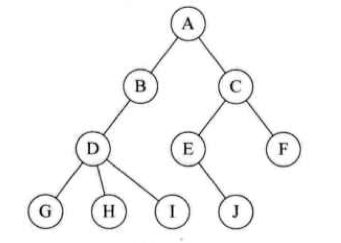
- 树是 n(n>=0) 个结点的有限集。n=0 时称为空树。在任意一棵非空树中:
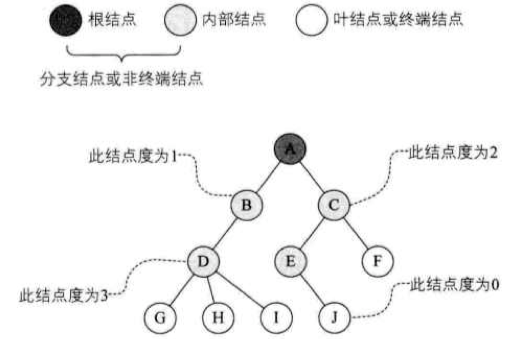
结点分类
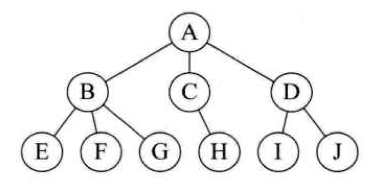
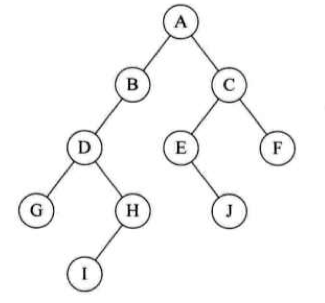
- 定义:结点拥有的子树数称为结点的度。度为 0 的结点称为叶结点或终端结点;度不为 0 的结点称为非终端结点或分支结点。除根结点外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。下面树结点的度的最大值是结点 D 的度,为 3,所以树的度也为 3 。
- 定义:结点拥有的子树数称为结点的度。度为 0 的结点称为叶结点或终端结点;度不为 0 的结点称为非终端结点或分支结点。除根结点外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。下面树结点的度的最大值是结点 D 的度,为 3,所以树的度也为 3 。
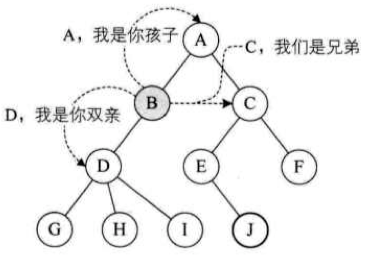
结点间关系
树的其他相关概念
结点的层次
从根开始定义起,根为第一层。
树中结点的最大层次称为树的深度或高度,下图树深度为 4
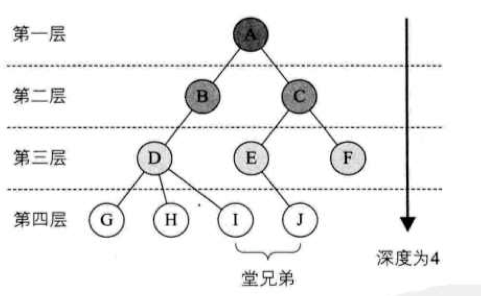
树与线性表结构的对比
阿萨德
二叉树
定义:二叉树是 n(n>=0)个结点的有限集合,该集合或为空集(称为空二叉树),或由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
特点:
- 每个结点最多有两棵子树
- 左子树和右子树是有顺序的,次序不能任意颠倒
- 即使树中某结点只有一棵树,也要区分左右子树
特殊二叉树
#斜树
- 定义:
- 所有结点都在左子树的二叉树叫左斜树
- 所有结点都在右子树的二叉树叫右斜树
- 所有结点都在左子树的二叉树叫左斜树
- 这种特殊树和线性表结构一样,所以线性表结构可以理解为是树的一种特殊形式
- 定义:
#满二叉树
#完全二叉树
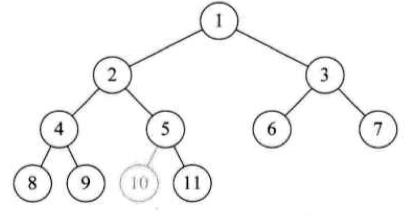
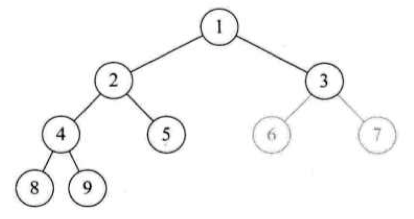
定义:对一棵具有 n 个结点的二叉树按层序编号,如果编号为 i (i <= i <= n) 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中的位置完全相同,则这课二叉树称为完全二叉树。
如何判定:在看树时,心中默默给每个结点按照满二叉树的结构逐层顺序编号,如果编号出现空挡,就说明不是完全二叉树,否则就是。
下面几个都不是:
9跟11之间有空挡
5跟8,9之间有空挡
9跟12之间有空挡
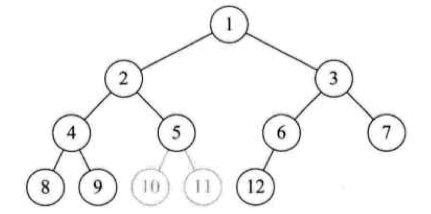
存储结构
- 二叉树顺序存储结构(适用于完全二叉树)
- 二叉链表
遍历二叉树
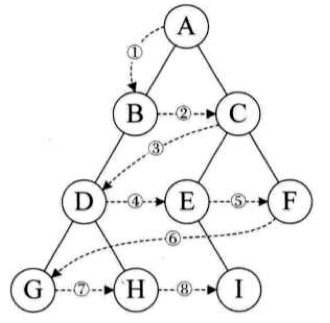
#二叉树遍历方法
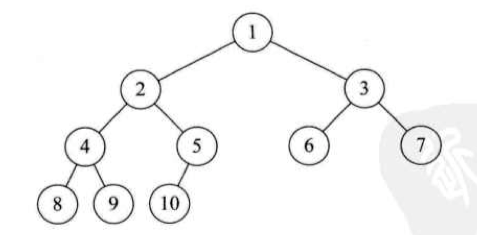
前序遍历
遍历顺序:ABDGHCEIF
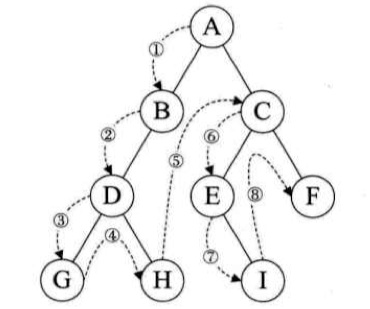
中序遍历
遍历顺序:GDHBAEICF
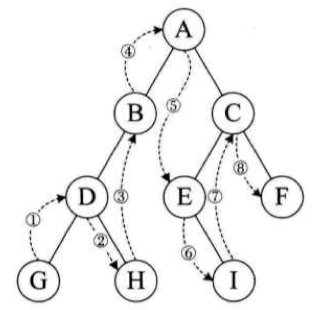
后序遍历
遍历顺序:GHDBIEFCA
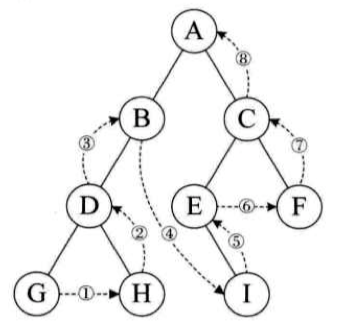
层序遍历
遍历顺序:ABCDEFGHI
图